Zbiory

Co nazywamy zbiorem?

Na przykład gdy weźmiemy wszystkie wasze skarpetki, jakie posiadacie i wrzucimy do jednego worka, wtedy będziemy mieli zbiór skarpetek
albo gdy kupimy paczkę papierosów, w niej mamy jakiś zbiór papierosów.

Są to po prostu pewne elementy w "worku"

Oczywiście nie jest to pełna definicja, ale tyle w tym temacie w zupełności wystarczy na poziomie szkoły ponadgimnazjalnej.

Oznaczenie:
zbiory oznaczamy dużymi literami: A,B,C,D,...
zaś ich elementy małymi: a,b,c,d
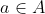-> czytamy: element a należy do zbioru A.

Przykładamy zbiorów, które Was obowiązują są:

(1) Liczby Naturalne 0,1,2,3,4,5, ... (czasami nie bierzemy zera jako liczbę naturalna, jest to "widzimi się" danego nauczyciela lub podręcznika. Tak i tak jest dobrze, wiec nie kłócić się z nauczycielem, jak powie Wam, że zero to nie jest liczba naturalna.

(2) Liczby Całkowite ...,-5,-4,-3,-2,-1,0,1,2,3,4,5,... są to po prostu liczby naturalne i liczby naturalne z przeciwnym znakiem.

(3) Liczby Wymierne - to takie liczby które jesteśmy w stanie zapisać za pomocą ułamka  , gdzie p oraz q są całowite.

(4) Liczby niewymierne, analogicznie - nie da się ich przedstawić w postaci ułamka  , gdzie p oraz q są całowite.
 Do takich liczb należą: 

(5) Liczby Rzeczywiste - które definiujemy jako zbiór wszystkich powyższych liczb.

Na powyższym schemacie występują nieco inne oznaczenia, niż te szkolne

N-liczby naturalne

Z- liczby Całkowite (od niemieckiego słowa Zahl-całość), w szkole możecie to oznaczać jako "C" - nikt Wam krzywdy nie zrobi.

Q- liczby wymierne, w szkole możecie oznaczać to jako "W"

IQ - liczby nie wymierne, w szkole "NW"

R- liczby rzeczywiste